平行四边形是最常见的特殊四边形之一,它的两组对边分别平行且相等,它的对角线互相平分,它的对角相等,为了利用这些性质,常常需要添加辅助线构造平行四边形。
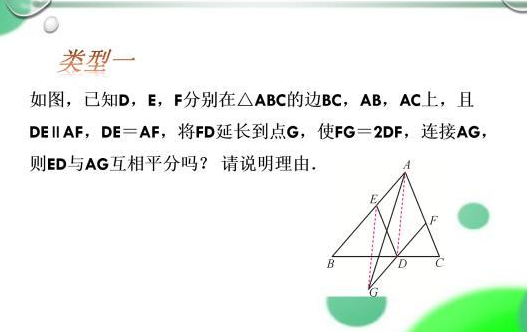
已知条件中涉及到平行,且要求证的结论中和平行四边形的性质有关,连接EG、AD构造平行四边形。∵DE∥AF,DE=AF,∴四边形AEDF是平行四边形.∴AE∥DF,AE=DF,又∵FG=2DF,∴DG=DF,∴AE=DG。又∵AE∥DG,∴四边形AEGD是平行四边形,∴ED与AG互相平分。
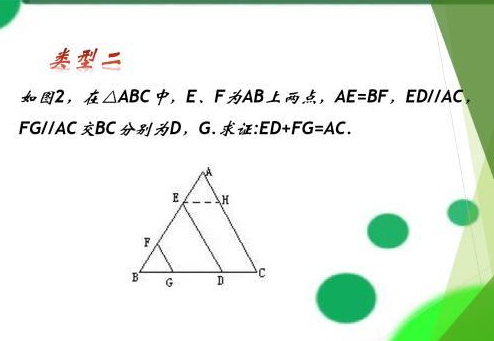
要证AC=ED+FG,首先应该想到截长补短,在结合已知条件中的DE∥AC,应该联想到过E作EN∥AC,这样不仅达到截长补短的目的,也构造出平行四边形BCNE。因为ED//AC,所以四边形CDEH是平行四边形,所以ED=HC,又FG//AC,EH//BC,所以∠AEH=∠B,∠A=∠BFG,又AE=BF,所以△AEH≌△FBG,所以AH=FG,所以FG+DE=AH+HC=AC。
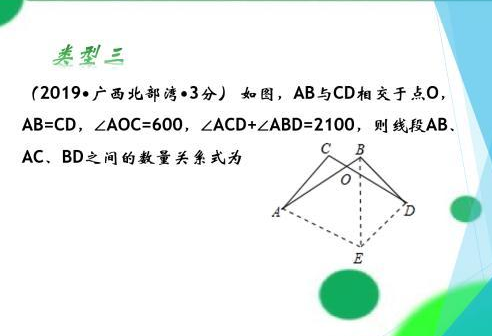
过点A作AE∥CD,截取AE=CD,连接BE、DE,则四边形ACDE是平行四边形,得出DE=AC,∠ACD=∠AED,证明△ABE为等边三角形得出BE=AB,求得∠BDE=360°-(∠AED+∠ABD)-∠EAB=90°,由勾股定理得出BE=DE+BD(注意两直角边的平方和等于斜边的平方,因为有的小伙伴看不到平方显示),即可得出结果。
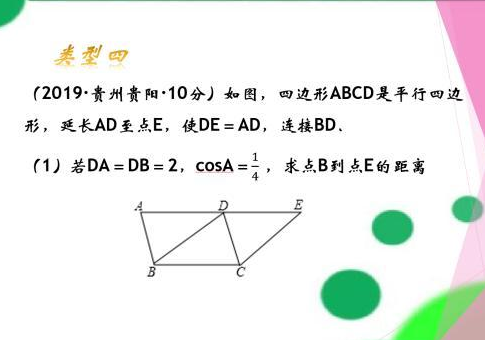
连接BE,根据已知条件得到AD=BD=DE=2,根据直角三角形的判定定理得到∠ABE=90°,AE=4,解直角三角形即可得到结论。
综上所述,不管是三角形,还是四边形,我们不难发现添加辅助线的方式都一样,无非是连接某两点、作平行或垂直、截长补短、延长;添加辅助线的目的都是构造出特殊图形,这也就是万变不离其宗。



